Introduction: Trueness, accuracy and precision
The words accuracy, trueness and precision are important differentiated terms when referring to measurements in the scientific and technical context. Generally speaking, accuracy refers to how close a measured value is in relation to a known value or standard. However, the International Organization for Standardization (ISO) uses “trueness” for the above definition while keeping the word “accuracy” to refer to the combination of trueness and precision. On the other hand, precision is related to how close several measurements of the same quantity are to each other. In the field of statistics it is rather common to use the terms “bias” and “variability” to refer to the lack of “trueness” and the lack of “precision” respectively.
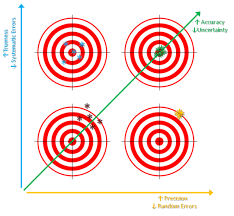
Figure 1: Picture showing the most accepted definitions of accuracy, trueness and precision.
How to culture vascularized & immunocompetent 3D models in a standard Multiwell
Accuracy and Trueness
The ISO standard 5725, under the title “Accuracy (trueness and precision) of measurement methods and results”, uses the combination of two terms, “trueness” and “precision” (Figure 1), to describe the accuracy of a measurement method. According to ISO 5725, “Trueness” refers to the closeness of agreement between the arithmetic mean of a large number of test results and the true or accepted reference value [1]. “Precision” refers to the closeness of agreement between different test results.
On the other hand, the Bureau International des Poids et Mesures (BIPM) defines accuracy as the closeness of agreement between a measured quantity value and a true quantity value of a measurand (quantity intended to be measured) [2]. In this case, trueness is defined as the closeness of agreement between the average of an infinite number of replicate measured quantity values and a reference quantity value. Equivalently, the New Oxford American Dictionary gives the technical definition of accuracy as the degree to which the result of a measurement, calculation, or specification conforms to the correct value or a standard [3]. In the same line, the Merriam-Webster dictionary defines accuracy as the degree of conformity of a measure to a standard or a true value [4].
As notated by the BIPM, historically, the term “measurement accuracy” has been used in related but slightly different ways. Sometimes a single measured value is considered to be accurate, when the measurement error is assumed to be generally small. In other cases, a set of measured values is considered to be accurate when both the measurement trueness and the measurement precision are assumed to be good. Care must therefore be taken in explaining in which sense the term “measurement accuracy” is being used. There is no generally established methodology for assigning a numerical value to measurement accuracy. In statistics, trueness is generally referred as lack of bias which is defined as the difference between an estimator’s expected value and the true value of the parameter being estimated. In some experimental cases, some external factors may change the measured value introducing a bias. The bias is defined as the difference between the mean of the measurements and the reference value. In general, the measuring instrument calibration procedures should focus on establishing and correcting it.
Precision Measurements
On the other hand, precision is defined, by the ISO standard 5725 [1], as the variability between repeated measurements (Figure 1). Generally speaking, tests performed on presumably identical materials in presumably identical circumstances do not, in general, yield identical results. This happens since the factors that influence the outcome of a measurement cannot all be completely controlled. All measurement procedures have inherent unavoidable random errors. If a measurement value differs from a specified value, which determines an expected property, in a range within the scope of unavoidable random errors, then a real deviation of the values cannot be established. This variability of the results is normally produced by the measurements environment, operator, equipment (including its calibration), and time period.
Equivalently, BIPM defines precision as the closeness of agreement between indications or measured quantity values obtained by replicate measurements on the same or similar objects under specified conditions [2]. Accuracy may include precision in its wider definition but the two words are not rigorously exchangeable.
Repeatability and reproducibility are included in the definition of precision and used for describing the variability of the measurement method. Generally speaking reproducibility incorporates more effects of influencing variability than repeatability. It is defined as the resulting variation of a measurement process when performed under different instruments, operators, environments, and time periods (conditions of measurement). On the other hand, repeatability refers to the variation arising even when efforts are made to keep constant the instrument, operator and environment, as well as to reduce the measuring time period.
Measurement precision, or more precisely imprecision, is defined numerically by standard deviation, variance, or the coefficient of variation.
Final remarks
A measurement device is both accurate and precise (or simply accurate, depending on the broad definition of this term) when it produces measurements all tightly clustered around the reference (“true”) value with a defined error range. The accuracy and precision of a measurement process are usually established by repeatedly measuring some traceable reference standard. Such standards are defined in the International System of Units (abbreviated SI from French: Système International (d’Unités)) and maintained by national standards organizations.
Tightly related to accuracy, trueness and precision, is the measurement error, also referred as an observational error. This error that can be quantified by different methods is defined as the difference between the “true” value and the measured value. The systematic part of the observational error is generally related to the trueness of the measurement while its random part is linked to precision.
References
- ISO 5725-1:1994. Accuracy (trueness and precision) of measurement methods and results — Part 1: General principles and definitions. 1994. https://www.iso.org/obp/ui/#iso:std:iso:5725:-1:ed-1:v1:en
- BIPM, Joint Committee for Guides in Metrology (JCGM), Working Group on the International Vocabulary of Metrology (VIM). International vocabulary of metrology — Basic and general concepts and associated terms (VIM), JCGM 200:2012. https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf
- In the New Oxford American dictionary (3rd Edition). 2010. https://en.oxforddictionaries.com/definition/accuracy
- In the Merriam-Webster’s dictionary (Nez Edition). 2016. https://www.merriam-webster.com/dictionary/accuracy
FAQ
The terms trueness and precision refer to different aspects of measurement. According to the International Organisation for Standardisation (ISO), "trueness" is defined as the closeness of agreement between the arithmetic mean of a large number of test results and the true or accepted reference value. "Precision," in contrast, is defined as the closeness of agreement found between different, independent test results. Precision, therefore, relates to the variability observed between repeated measurements. In statistics, a lack of trueness is commonly referred to as "bias". A lack of precision is described as "variability". It is noted that tests performed on identical materials under identical circumstances generally do not produce identical results. This is because the factors that influence the measurement’s outcome cannot all be completely controlled.
The word "accuracy" is used in related but slightly different ways. The International Organisation for Standardisation (ISO) standard 5725 uses "accuracy" to describe the combination of both "trueness" and "precision". In this context, accuracy is the overall term. Conversely, the Bureau International des Poids et Mesures (BIPM) defines accuracy as the closeness of agreement between a single measured quantity value and a true quantity value of the item being measured. Dictionaries provide similar technical definitions, describing accuracy as the degree to which a measurement conforms to a standard or a correct value. The BIPM suggests that care must be taken to explain which sense of the term is being used. Sometimes it refers to a single measurement, while in other cases it refers to a set of measurements where both trueness and precision are assumed to be good.
In statistics, the term "bias" is used to refer to a lack of trueness. Bias is formally defined as the difference between an estimator’s expected value and the true value of the parameter that is being estimated. In some experimental setups, external factors can change the measured value, which introduces a bias. This bias is calculated as the difference between the mean of the measurements and the reference value. While there is no single established methodology for assigning a numerical value to accuracy, bias can be managed. It is generally intended that calibration procedures for a measuring instrument should focus on establishing and correcting this bias. The systematic part of any measurement error is usually related to the trueness, or bias, of the measurement.
Both repeatability and reproducibility are concepts included within the definition of precision. They are used to describe the variability of a measurement method. Reproducibility is defined as the variation in a measurement process that occurs when it is performed under different conditions. These differing conditions include different instruments, operators, environments, or time periods. Reproducibility is said to incorporate more factors of variability than repeatability. Repeatability, by contrast, refers to the variation that arises even when efforts are made to keep all conditions constant. This means the measurement is performed with the same instrument and operator, in the same environment, and within a short time period.
Measurement precision, or more specifically imprecision, is quantified numerically. It is expressed using the standard deviation, the variance, or the coefficient of variation. A related concept is measurement error, also called observational error. This is defined as the difference between the "true" value and the measured value. This error is composed of two parts. The systematic part of the error is related to the measurement’s trueness, or bias. The random part of the error is linked to the measurement’s precision. All measurement procedures have unavoidable random errors. If a measured value’s deviation from a reference value is within the scope of these random errors, a true deviation cannot be established.